minimum

dans la figure ,  (AC) et (BD)  sont toutes les deux perp à (CD) AC=3 CD=6 et BD=2
M un point de [CD] , on pose CM=x
1) calculer MA+MB en fonction de x
2) soit f la fonction f(x)=MA+MB
montrer à partir d'une construction graphique l'existence d'un pt M minimisant la somme cherchée
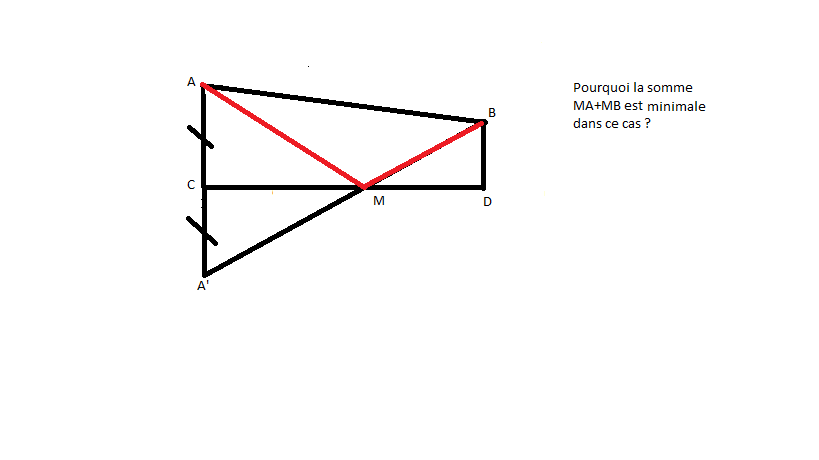
3) soit A' le symétrique de A par rapport à C . expliquer pourquoi le point M cherché est aligné avec A' et B
4) en déduire le réel x définissant le pt M cherché

1) MA+MB= (x²+9) + [4+(6-x)²] , x[0,6]  
2) j'ai construit f sur [0,6] et j'ai trouvé qu'elle décroissante puis croissante donc il y a un point M minimisant la somme MA+MB
3) je veux ici savoir si c'est juste :
Quelle que soit la position du point M, on a  AM + MB = A'M + MB .
A'MB décrit un triangle lorsque M n'app pas à [A'B] alors d'après l'inégalité triangulaire on a ,
A'M+MB>=AB par suite lorsque A'M+MB=AB ( c'est à dire M app à[AB] ) on a une valeur minimale de AM + MB
c'est ça ?

4) c'est du calcul

merci pour votre aide

Bonsoir,

Dans la première question, il manque des carrés pour que tes résultats soient juste.

En effet, MA²+MB² donne bien le résultat que tu proposes mais sinon, il manque les racines carrées pour que tout soit exact s'il s'agit bien de MA + MB.
Il n'empêche qu'il te manque les justifications de tes résultats (théorème de Pythagore dans deux triangles)

Pour la construction graphique de F c'est une évidence de conclure en effet.

Pour la question suivante, il s'agit de la propriété de 5ème qui dit que l'inégalité triangulaire est une égalité si et seulement si les trois points sont alignés.

L'avant dernière question, permettant d'avoir l'alignement des points et sachant qu'il y a des parallèles, le théorème de Thalès s'applique et on en déduit la valeur de x directement.

Bonne continuation!