Correction de DS

Bonjour!

J'ai besoin de votre aide pour corriger un DS.
N'ayant pas été fameux, notre prof' a décidée de nous mettre la correction en DM à rendre pour mercredi!

Voici le sujet:


Voici ce que j'ai commence à faire:

1)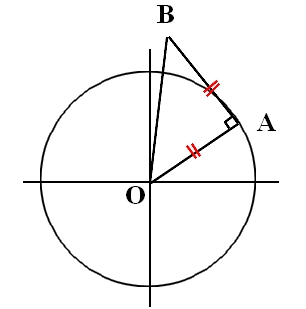
Dsl le dessin est très approximatif vu que je le fais sur l'ordi'.

2) R_b = OB = rOA
OB et OA sont des vecteurs.

OAB est isocèle donc (OA,OB) = Pi/4

Téta_b = (I,OB) = (I,OA) + (OA,OB)
= Téta + Pi/4

Les coordonnées polaires de B dans le repère (O,I) sont (rOA, Téta+Pi/4)

3) Voici ce que j'ai fais sur ma copie: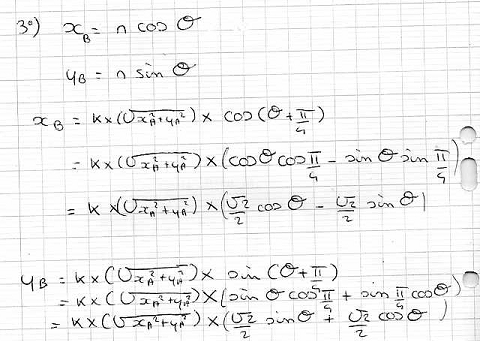



Merci de votre aide!

Bonsoir Nicolas,

Ton dessin est très bien fait ne t'inquiète pas.

Pour la question 2), ton angle est tout à fait juste car le triangle est direct et isocèle rectangle en effet. Par contre comment calcules-tu la distance OB, je ne saisi pas très bien vu que tu donne le résultat en fonction de OA alors qu'on sais que OA=r et quel e résultat ne doit dépendre que de r et de thêta.

Pour ce faire n'oublie pas une propriété fondamentale dans le triangle rectangle .

La question 3 découle de la question 2), en effet, la relation entre les coordonnée polaire et cartésiennes sont quasi immédiate mais par contre il va falloir trouver la bonne distance OB pour que cette question soit juste ce qui plombe ton calcul en fait.

Bon courage et n'hésite pas à poser des questions si ce que je dis n'est pas clair!

Heu... Je vois peut être ce que vous voulez dire...

2) R_B = OB = kOA = k*r_A
OB et OA sont des vecteurs.

OAB est isocèle et rectangle en A, donc:

OB²=OA²+BA²
=r_A²+r_A²
=2r_A²
=√2r_A

R_B=√2r_A

θ_B = (I,OB) = (I,OA) + (OA,OB)
= θ + Pi/4

Les coordonnées polaires de B dans le repère (O,I) sont (√2r_A, Téta+Pi/4)

C'est cela ?

Si tu m'enlève ça:

Citation :

R_B = OB = kOA = k*r_A
OB et OA sont des vecteurs.

Tout est jsute en effet.

Car comment OB pour être colinéaire à OA alor qu'il n'ont même pas la même direction .

Donc on a bien l'utilisatino du théorème de pythagore dans le triangle rectangle en A (il fautl e marquer sur une copie pour que le correcteur sache ce que tu fais concrètement, celà permet de suivre la démarche et d'y mettre des points ce qui n'estp as négligeable . Celà permet aussi pour toi de suivre la cohérence de ton raisonnement et de ta rédaction ce qui est un plus.)

On a bien: Les coordonnées polaires de B dans le repère (O,I) sont (r_A√2, Téta+Pi/4)

Alors maintenant coment fait-on la question suivante?

J'ai un peu bossé dessus... Je vois que cela...



Dsl j'ai pas eu le courage de tout réécrire sur l'ordi'... :S

Il n'y a que pour X de B.

Bonsoir,

L'expression en fonction des coordonnée cartésienne de A est juste. Par contre l'expression cartésienne en fonction des coordonnée polaire de A est erronée.

En effet, ce que tu écrit est plutôt de la forme:

x_B=r_B*Cos(θ_B)
y_B=r_B*Sin(θ_B)


Mettre les indices aide à savoir de quoi ont parle et évite donc les erreur plus bêtes que méchante lors d'un devoir .

Je te laisse donc reprendre la première partie et finir l'expression de y_B en fonction des coordonnées cartésienne de A.

Bon courage!

Heu... Je n'arrive pas à distinguer mon érreur...

Il est logique que ce que j'ai fais sois de la forme:

xB=rB*Cos(θB)
yB=rB*Sin(θB)

Vu que R_b=√2r_A=√2*(√x_A²+y_A)...

Enfin je ne sais pas...

C'est logique en effet vu qu'il s'agit de la définition .

Mais le soucis c'est que notre réponse doit être en fonction de r et θ (c'est à dire r_A et θ_A) or ce n'est pas le cas.

Donc l'erreur n'est pas dans la forme de la réponse mais plutôt dans la réponse par rapport à l'énoncer de la question tout simplement. Pour mettre sous la deuxième forme avec les coordonnées cartésiennes de A c'est nickel, il n'y a rien à redire de ce point de vu là.


Est-ce que tu comprends mieux ton erreur?

Ah oui peut être... Donc:

x_B=r_B*Cos(θ_B)
=√2r_A*Cos(θ_A+Pi/4)
=√2r_A*(Cos(θ_A)Cos(Pi/4)-Sin(θ_A)Sin(Pi/4))
=√2r_A*(√2/2*Cos(θ_A)-√2/2*Sin(θ_A))
=√2r_A*√2/2*Cos(θ_A)-√2r_A*√2/2*Sin(θ_A)
= r_A*Cos(θ_A)-r_A*Sin(θ_A)

Bon voila encore une fois ce n'est que pour X! ^^'

Bonne nuit... ^^

C'est tout à fait ça.

Tu pouvais même le laisser sous la forme x_B=r*√2*Cos(θ+Pi/4) sans pour autant développer le tout mais la forme totalement développée t'avance dans les calculs pour repasser avec les coordonnées cartésiennes de A.

Bon courage pour la suite!

Re'! ^^

J'ai donc commencé l'exercice 2.

La 1er question, je l'ai eu juste. Mais je bloque sur la 2eme... Pouvez vous m'aider s'il vous plais ? ^^

Bonsoir,

La première question n'est pas anodine et elle va donc servir dans la deuxième question mais on ne voit pas très bien comment dans un premier temps. Donc pour le moment, on sait juste que M, N et B sont alignés, donc le fait que B puisse être le milieu de [MN] pour une certaine valeur de α c'est envisageable vu qu'on a déjà l'alignement.

Bon maintenant, qu'est-ce que celà apporterait de plus pour la figure si B est le milieu de [MN]? Autre question pour te faire sentir la chose, que sait-on du triangle MNC ?

Bon courage!

Pour que B soit le milieu de [MN], il faudrait que BC soit une bissectrice du triangle MNC. (De l'angle (CN,CM))

C'est cela ?

Non ce n'est pas une bissectrice.

Qu'elle estl a nature du triangle MNC et que signifie que B soit le milieu de [MN] dans de genre de triangle?

Une médiane ? >_<

C'est une médiane en effet issue de C exactement.

Mais une médiane issue de C dans quel genre de triangle? Qu'est-ce qu'il a de particulier ce triangle MNC d'après les hypothèses?

C'est un triangle rectangle... Donc il divise l'angle en deux ce qui fait deux angles de Pi/4.

Donc après vu que l'on sait que la somme des angles d'un triangle est de Pi, alors:

Alpha=Pi-((BA,BC)+(CB,CA))
=Pi-3Pi/4
=PI/4

Donc l'angle Alpha devra être de Pi/4 pour que B soit le milieu de [MN]?

Le triangle est rectangle en effet mais je t'avais précisé tout à leur qu'il ne s'agissait pas d'une bissectrice Sauf si CN=CM ce qui n'est pas précisé ici.

Par contre, le triangle est rectangle en C, donc [MN] est l'hypothénus de notre triangle rectangle ABC. Que sait-on du milieu de l'hypothénus d'un triangle rectangle?

Par concéquent que savons-nous de la longueur BC par rapport à la longueur BN par exemple?

Raaa... Je suis un cas désespéré.

Elles sont égales ?...

Mais non t'es pas un cas désespéré sinon je serait parti me couché y'a longtemps .

En effet, elles sont égales mais t'as pas l'air convaincu.

Tout triangle rectangle est inscriptible dans un demi cercle de diamètre l'hypothénus! Du coup le milieu de l'hypothénus c'est le centre du cercle circonscrit au triangle et vu que le cercle circonscrit au triangle passe par tous les points du triangle, on a bien:

BN=BM=BC vu que BMN est rectangle en C et qu'on suppose que B est le milieu de [MN].


Cette propriété là est a connaître par coeur!!!! Tu l'as marque sur une feuille ne fluo et tu l'accroche au-dessus de ton lit pour la lire tous les soir si il le faut mais cette propriété des triangle rectangle est vraiment incontournable.

Bon maintenant qu'on sait que BC=BN, que savont nous ne plus sur BC par hyptohèse dans l'énoncer?

Qu'en déduit-on pour le triangle BNC (toujours sous la condition B milieu de [MN]) ?

BC=CN

Donc le triangle BCN est équilatéral.

La petite fiche est accrochée ^^'

Yes !!

Notre triangle est donc équilatéral. C'est génial ça non? Qu'est-ce qu'on sait des angles d'un triangle équilatéral? Qu'a-t-on calculer dans la question 1)?

Qu'en déduit-on pour la valeur de notre angle alpha??

Tout s'enchaîne maintenant , il ne faut jamais perdre de vu ce qu'on cherche tout en sachant ce qu'on a et ce qu'on veut pour y arriver.

Ah... Je comprend, je comprend... Il serait temps! ^^'

Ouais donc vu que les angles d'un rectangle équilatéral sont de PI/3 alors l'angle Alpha sera de 5Pi/6 si l'on veut que le point B soit le milieu de [MN]. C'est cela ?

5*Pi/6 ?


Si alpha= 5*Pi/6 celà signifie que l'angle (CB,CA)= Pi/2 - 5*Pi/6 (car le triangle ABC est rectangle en B donc la sommes des angles de la base fait Pi/2)

C'est à dire que l'angle (CB,CA)= (3*Pi - 5*Pi)/6 = -2Pi/6= -Pi/3

Or l'orientation de mon angle est direct dans il devrait être positif. J'en conclu qu'il y a une erreur dans ton calcul .


Alors qu'avais-tu trouvé dans la question 1) pour l'angle: (BC,BN) en fonction de alpha?

On y est presque mais une erreur de calcul subsiste encore et ça fait capoté tout le beau raisonnemetn, ça serait dommage de ne pas pouvoir finir après un dur labeur pour en arrivée là.

C'est bon j'ai vu mon erreur... Je me suis pressé de finir et j'ai fais n'importe quoi...

Donc je trouve Alpha=2Pi/6 ^^