 | Maths Cuicui, l'envolée mathématique
forum gratuit d'entraide mathématique de la 6ème à bac+2
|
|
| | Limite |  |
| | | Auteur | Message |
|---|
Eh
 Nombre de messages : 237 Nombre de messages : 237
Localisation : France
Date d'inscription : 08/02/2009
 |  Sujet: Limite Sujet: Limite  Dim 3 Jan - 17:58 Dim 3 Jan - 17:58 | |
| Salut ! J'ai un petit problème avec cette limite (je te l'ai tappé avec Latex pour plus de visibilité) : 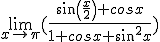 J'ai réussi à prouver qu'elle valait 1/4 avec le théorème de l'Hospital mais bon faut avouer que c'est de la triche ^^ Aurais-tu des pistes à me donner ? Merci d'avance. | |
|   | | Blagu'cuicui
Admin'cuicui

 Nombre de messages : 5146 Nombre de messages : 5146
Age : 38
Localisation : Bretagne (35)
Date d'inscription : 03/09/2007
 |  Sujet: Re: Limite Sujet: Re: Limite  Dim 3 Jan - 18:16 Dim 3 Jan - 18:16 | |
| Bonsoir et bonne année 2010!
Alors, on peut essayer de s'en sortir en améliorant l'expression d'une part. En effet, nous avons des cosinus et des sinus. Donc l'idée générale est de se ramener à un polynôme en cosinus ou en sinus pour ainsi effectuer un changement de variable et s'en sortir donc.
Il s'avère ici que c'est tout à fait faisable en plus. En effet, essaie d'arriver à un polynôme en Sin(x/2) aussi bien au numérateur qu'au dénominateur. Ensuite, on va effectuer le changement de variable X=Sin(x/2) avec la limite lorsque X tend vers 1 donc.
Je te laisse découvrir la suite pour l'instant.
Bon courage! (faut mettre les mains dans le cambouis là). | |
|   | | Eh
 Nombre de messages : 237 Nombre de messages : 237
Localisation : France
Date d'inscription : 08/02/2009
 |  Sujet: Re: Limite Sujet: Re: Limite  Dim 3 Jan - 18:48 Dim 3 Jan - 18:48 | |
| Ok, donc en espérant de ne pas avoir fait de faute, et après avoir opéré le changement de variable X = sin(x/2), j'obtiens :
lim en 1 de (-2X²+X+1)/(-4X4+2X²+2) donc en simplifiant en haut et en bas par (X-1) on trouve bien -3/-12 = 1/4.
Est-ce bon ?
Aurais-t-on pu effectuer un autre changement de variable ?
Y-a-t-il une autre méthode ? | |
|   | | Blagu'cuicui
Admin'cuicui

 Nombre de messages : 5146 Nombre de messages : 5146
Age : 38
Localisation : Bretagne (35)
Date d'inscription : 03/09/2007
 |  Sujet: Re: Limite Sujet: Re: Limite  Dim 3 Jan - 19:08 Dim 3 Jan - 19:08 | |
| C'est tout à fait exacte !!
Une autre méthode, je ne pense pas pour le coup car la difficulté résidait dans le Sin(x/2) qui était le seul à avoir l'image de x/2. Il fallait donc tout ramener à cette image là. Ensuite, pourquoi le sinus? Car passer du Sin(x/2) à un cosinus cela n'est pas forcément simple sans avoir la facilité de la relation fondamentale Cos²+Sin²=Id. Donc autant faire simple.
Je ne vois pas d'autre méthode pour ma part en tout cas. Intuitivement, c'est une méthode plutôt logique le changement de variable lorsqu'on a des cosinus ou des sinus (et qu'on n'a pas explicitement des taux d'accroissement bien entendu). La méthode de l'Hospital est bien sûr massue ici. Mais en temps, pas sûr qu'elle soit plus rapide. Après en difficulté de calcul, je ne sais pas, il faut dériver deux fois ici des fonctions trigonométriques de surcroît et des produits aussi si on se démerde mal. Donc pas convaincu que cela soit plus simple en fait. Par contre, cette règle est plus automatique, je te le concède tout à fait par rapport à la réflexion qu'il faut suivre pour arriver à penser au changement de variable puis trouver le bon et enfin faire les calculs sans se planter.
Bon courage pour la suite!
Dernière édition par Blagu'cuicui le Lun 4 Jan - 22:40, édité 1 fois (Raison : orthographique) | |
|   | | Eh
 Nombre de messages : 237 Nombre de messages : 237
Localisation : France
Date d'inscription : 08/02/2009
 |  Sujet: Re: Limite Sujet: Re: Limite  Lun 4 Jan - 22:19 Lun 4 Jan - 22:19 | |
| Ah si quand même avec l'hospital c'est bien plus rapide ici... | |
|   | | nulenmath
Nombre de messages : 43
Localisation : ile de france
Date d'inscription : 17/02/2010
 |  Sujet: limite et variation Sujet: limite et variation  Dim 28 Fév - 0:36 Dim 28 Fév - 0:36 | |
| afin d'éviter de créer trop de topic, je me permet de poster ici.
je voudrais savoir, s'il est possible sans tableau de variation, de connaître les variations d'une courbe d'une fonction à l'aide des limites.
cordialement. | |
|   | | Blagu'cuicui
Admin'cuicui

 Nombre de messages : 5146 Nombre de messages : 5146
Age : 38
Localisation : Bretagne (35)
Date d'inscription : 03/09/2007
 |  Sujet: Re: Limite Sujet: Re: Limite  Dim 28 Fév - 12:39 Dim 28 Fév - 12:39 | |
| Bonjour,
Tu aurais dû te permettre de créer un autre sujet car ta question est un classique en soi. En effet, il est impossible de connaître les variations d'une fonction uniquement en regardant les limites au bords de l'intervalle.
En effet, si je te dis que je considère une fonction F définie sur un intervalle [a,b] et dont la limite en a est +∞ par exemple et en b, -∞. Je considère qu'avec seulement ces informations, tu es capable de me tracer une infinité de courbe vérifiant ces deux limites avec des variations toutes différentes.
Par contre un moyen de ne pas passer par le tableau de variation c'est de considérer des compositions de fonctions car dans certains cas si on connaît les variations des fonctions élémentaires, nous pouvons en déduire les variations de leur composée. Enfin, un autre moyen de ne pas faire de tableau de variation c'est de revenir à la définition de la croissance ou de la décroissance en essayant de regarder si les images sont dans le même ordre que leurs antécédents par exemple (ce qu'on fait en seconde lorsqu'on n'a pas encore la dérivation par exemple).
Est-ce que cela te paraît plus claire?
Bon courage!
Dernière édition par Blagu'cuicui le Dim 28 Fév - 17:54, édité 1 fois (Raison : orthographique) | |
|   | | nulenmath
Nombre de messages : 43
Localisation : ile de france
Date d'inscription : 17/02/2010
 |  Sujet: Re: Limite Sujet: Re: Limite  Dim 28 Fév - 17:23 Dim 28 Fév - 17:23 | |
| okay merci pour la réponse, de toute façon je suis passé par la dérivée et j'ai réussi ce que je voulais.
par contre je n'ai pas très bien compris cette explication : "Enfin, un autre moyen de ne pas faire de tableau de variation c'est de revenir à la définition de la croissance ou de la décroissance en essayant de regarder si les images sont dans le même ordre que leurs antécédents par exemple (ce qu'on fait en seconde lorsqu'on n'a pas encore la dérivation)". | |
|   | | Blagu'cuicui
Admin'cuicui

 Nombre de messages : 5146 Nombre de messages : 5146
Age : 38
Localisation : Bretagne (35)
Date d'inscription : 03/09/2007
 |  Sujet: Re: Limite Sujet: Re: Limite  Dim 28 Fév - 18:04 Dim 28 Fév - 18:04 | |
| En fait la définition de base de la variation d'une fonction est indépendante de la dérivation d'une fonction. En fait, la dérivation fait appel tout de même à la notion de limite et donc infiniment proche ce qui est loin d'être évident d'un premier abord alors qu'on a pourtant cette facilité à lire sur une courbe si celle-ci est croissante ou non pas exemple.
Donc en fait, on utilise pour introduire la notion de variation une définition plutôt élémentaire et surtout très intuitive vu qu'on peut la retrouver ne lisant un graphique par exemple. Et celle-ci est la suivante:
Soit F une fonction définie sur un intervalle I (l'intervalle étant fini ou pas d'ailleurs)
Si pour tout a, b dans l'intervalle I tels que a≥b, on a: F(a)≥F(b) (les images de a et b par la fonction F sont rangées dans le même ordre que a et b)
Alors F est croissante sur I
De même, on a la stricte croissance si pour tout a>b, on a: F(a)>F(b).
Pour la décroissance, les images sont rangées dans l'ordre inverse de leur antécédent c'est à dire:
Si pour tout a, b dans I tels que a≥b, on a: F(a)≤F(b)
Alors F est décroissante sur I
Et c'est avec cette définition là, qu'on travaille à la base. En effet, la notion de dérivée positive par exemple va en fauit vérifier la première définition sur la croissance et c'est pour celà qu'on dit que si la dérivée d'une fonction est positive alors la fonction est croissante. En fait, il y a même équivalence entre les deux (dérivée et définition élémentaire).
Est-ce plus claire ainsi?
Bon courage pour la suite! | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Limite Sujet: Re: Limite  | |
| |
|   | | | | Limite |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
|





